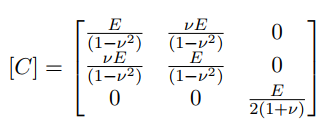octave 基本操作

算数运算的符号：+,-,*,/,^,()

注释用%标出，行内行间注释方法相同。

普通的函数:
sin, cos,tan,asin, acos,atan,exp,log,sqrt,abs

矩阵：[ ] 【行间用；隔开】

矩阵计算使用的符号：+,-,*,,’

有限元计算的原理

1. 最简单的情况

1.1 一维杆两端受力：

已知杨氏模量E，横截面积A，杆的长度L。

有杆两端的位移（u1,u2）和力（F1,F2）,可以通过物理公式求得刚度矩阵。

1.2 一维杆中间+一端受力：

已知杨氏模量E，横截面积A，杆的长度L，力的位置。

有施加的两个力的方向和大小，求结点位移。

1.3 一维变截面杆中间两处受力

已知杨氏模量E，横截面积A1、A2，杆的长度L，力的位置。

求结点位移和两端的支持力。


2与3横截面积相同：

从以上几个例子中可以看出，力与位移之间存在正相关关系，系数即为单元刚度矩阵。在越来越复杂的受力情况中，我们通过分段（有限元法）求出答案。

2. 能量法

能量法的适用范围更广，比方说有弹性形变的问题。

2.1 伸长量与位移线性相关

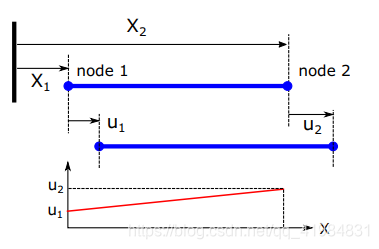
线性形函数可以表示为：



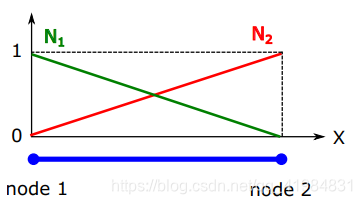
在local坐标系之下，X的函数可以表示为x的函数：


这时候力就由位移对位置的导数得出。

计算应变能：

其中E和A可以是x的导数。

单元刚度：

2.2 横截面积是x的函数的情况

各自积分求和。

2.3 施加外部力

在点1处施加外部力R1：

在点2处施加外部力R2：

引起的势能：

2.4 施加外部牵引力（这里指的是，施加沿杆方向大小变化的连续力）

和2.3不同的是这一步需要积分计算：

总能量：

存在这样的关系：

3. 高斯积分

尽管从全局坐标更换到local坐标不难，但有时候求积分也是挺难的。这时候就要用到高斯积分来近似一下，简化计算过程。这是计算机采用的方法。

仍需注意：N个高斯点能求解2N-1阶的精确结果。

高斯表：

3.1 intrinsic 坐标

即坐标范围在[-1，1]之间，和local坐标是线性对应关系。

3.2 高斯积分计算T(x)变化的情况

已知杨氏模量E，横截面积A，杆的长度L。
题面：

i：

用一个高斯点：


用两个高斯点：


可见一个高斯点足以达到精确值。

ii：

用一个高斯点：


用两个高斯点：


这里两个高斯点才是准确值。

3.3 用分段解决问题

已知杨氏模量E，横截面积A，杆的长度L。

其中T(x)为常数。

分两段：

连接矩阵：

分三段：

连接矩阵：